Sine and Cosine Rules: Worksheet, Formulae & Examples

Understanding the sine and cosine rules is crucial in mastering triangle geometry, especially in trigonometry and A-Level mathematics. These rules help solve non-right-angled triangles, allowing students to calculate missing sides or angles when traditional SOHCAHTOA methods fall short. Whether you’re a student preparing for exams or a teacher creating engaging resources, this blog post will provide formulas, solved examples, and a free downloadable worksheet to deepen your understanding.

Historical Background of Sine and Cosine Rules

The sine and cosine rules trace back to ancient Greek and Indian mathematicians. The sine rule appears in early trigonometric work by Aryabhata and Ptolemy, while the cosine rule has roots in Euclidean geometry, formally introduced during the Islamic Golden Age. These rules were essential in astronomical calculations and later formalized into modern trigonometry.

What Is the Sine Rule? (Law of Sines)

The sine rule relates the sides of a triangle to the sines of their opposite angles:

\[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \]

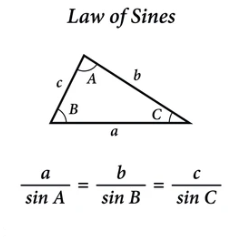
When to Use:

When you know two angles and one side (AAS or ASA)
When you know two sides and a non-included angle (SSA)

Solved Examples: Sine Rule

In triangle ABC, A = 30°, B = 45°, and a = 10 cm. Find side b.

\[ \frac{10}{\sin 30} = \frac{b}{\sin 45} \Rightarrow b \approx 14.14 \, \text{cm} \]

2. In triangle XYZ, angle X = 50°, angle Z = 65°, and side x = 12 cm. Find side z.

\[\dfrac{12}{\sin 50}=\dfrac{z}{sin65}\Rightarrow z=14.47cm\]

3. In triangle PQR, angle P = 40°, angle Q = 60°, and side p = 8 cm. Find side q.

\[\dfrac{8}{\sin 40}=\dfrac{q}{\sin 60}\Rightarrow q=10.26cm\]

What Is Cosine Rule? (Law of Cosines)

The cosine rule generalizes the Pythagorean theorem for non-right-angled triangles:

\[c^{2}=a^{2}+b^{2}-2ab\cos \left( ACB\right)\]

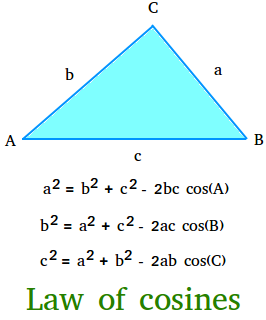
It is rearranged to find angles:

\[\cos \left( ACB\right) =\dfrac{a^{2}+b^{2}-c^{2}}{2ab}\]

When to Use:

When you know two sides and the included angle (SAS)
When you know all three sides (SSS)

Solved Examples: Cosine Rule

In triangle ABC, side a = 7 cm, side b = 10 cm, angle C = 60°. Find side c.

\[c^{2}=7^{2}+10^{2}-2\times 7\times 10\times \cos 60\Rightarrow c=8\cdot 89cm\]

2. In triangle XYZ, side x = 6 cm, side y = 8 cm, angle Z = 45°. Find side z.

\[z^{2}=6^{2}+8^{2}-2\times 6\times 9\times \cos 45\Rightarrow z=5.66cm\]

3. In triangle PQR, side p = 5 cm, side q = 9 cm, angle R = 70°. Find side r.

\[r^{2}=5^{2}+9^{2}-2\times 5\times 9\times \cos 70\Rightarrow r=8\cdot 67cm\]

Sine And Cosine Rules: Downloadable Practice Worksheet (PDF)

Want more practice? Download this free resource with 20 mixed questions and answers:

👉 Download Sine and Cosine Rule Worksheet (PDF)

10 Sine Rule questions
10 Cosine Rule questions
Answers included (no worked solutions)

Why Learn with My Maths Club?

At My Maths Club, we offer expert-led online tuition in:

IGCSE Math (0580 & 0606)
O-Level Math Syllabus D (4024)
A-Level Maths (9709): Pure Mathematics, Mechanics, and Statistics

📘 All our students receive:

Free eBooks & worksheets
Topical past paper packs
AI-powered quizzes
Recordings of all live classes

➡️ Explore our A-Level Math Tuition ➡️ Join IGCSE Math Classes

In summary, mastering the sine and cosine rule equips you to tackle any triangle with confidence. Whether you’re preparing for exams or want to improve your geometry skills, our examples, formulas, and worksheet will help.

For structured lessons and professional support, consider joining My Maths Club today!