Piecewise Function | How to graph a piecewise function?

What is a Piecewise Function?

Certain functions are defined differently in different parts of their domain and are thus more naturally expressed in terms of more than one formula. We refer to such a function as a piecewise function or a piecewise-defined function. Piecewise functions will be useful to us in the study of limits, continuity, and the derivative as examples and counterexamples of functions having certain properties.

Table of content

If you don’t find enough time to complete this article in a single read, make sure to BOOKMARK this page for future saturation if you don’t want to miss this useful content.

Examples: How to Graph a Piecewise Function?

Example#1

Let f be the function defined by;

\[f\left( x\right) =\begin{cases}x-1,\space\space\space x <3\\ 5,\space\space\space x=3\\ 2x+1,\space\space\space3 <x\end{cases}\]

Determine the domain and range of f, and sketch its graph.

Solution:-

The domain of f is (-∞, +∞), the following figure shows the graph of ‘f’;

it consists of the portion of the line y=x-1 for which x<3, the point (3,5), and the portion of the line y = 2x+1 for which 3<x. The function values are either numbers less than 2, the number 5, or numbers greater than 7. Therefore the range of f is the number 5 and the numbers (-∞, 2) ∪ (7, +∞).

Example#2

Let g be the function defined by;

\[f\left( x\right) =\begin{cases}3x-2,\space\space\space\space x < 1\\ x^{2}, \space\space\space\space\space 1\leq x\end{cases}\]

Determine the domain and range of g, and sketch its piecewise graph.

Solution:-

The domain of g is (-∞, +∞), following is the graph of the function;

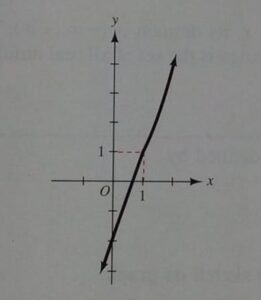
The graph contains the portion of the line y= 3x-2 for which x<1 and the portion of the parabola y = x² for which 1 ≤ x. The range is (-∞, +∞).

Example#3

The H is the function defined by;

\[H\left( x\right) =\begin{cases}x+3, \space\space\space\space x\neq 3\\ 2, \space\space\space\space x=3\end{cases}\]

Determine the domain and range of H and sketch its graph.

Solution:-

As H is defined for all x, its domain is (-∞, +∞), the graph is sketched below;

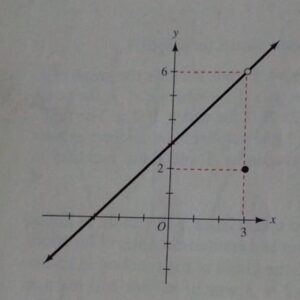
The range is the set of all real numbers except 6, so in terms of set, we can express range as ℝ-{6}.

Example#4

The piecewise function f is defined by;

\[f\left( x\right) =\begin{cases}x^{2}, \space\space\space\space x\neq 2\\ 7, \space\space\space\space x=2\end{cases}\]

Determine the domain and range of f and sketch its graph.

Solution:-

Because f is defined for all x, the domain is (-∞, +∞). The graph appearing below;

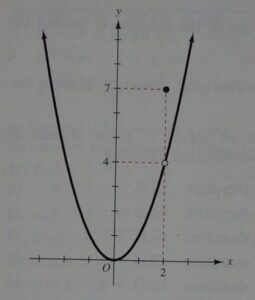
How to graph piecewise function through graphing calculator

consists of the point (2, 7) and all the points on the parabola y = x² except (2, 4). The range is [0, +∞).

Example#5

Determine the domain and range of the absolute value function ‘f’ for which f(x) = |x| and sketch its graph.

Solution:-

From the definition of absolute value function |x|, f(x) is defined piecewise function as below,

\[f\left( x\right) =\begin{cases}x, \space\space\space\space x\geq 0\\ -x, \space\space\space\space x <0\end{cases}\]

The domain is (-∞, +∞). The graph of ‘f’ consists of two half-lines through the origin and above the x-axis.

one has slope 1 and the other has slope -1. The range is [0, +∞).

Example#6

The piecewise function f is defined by;

\[f\left( x\right) =\begin{cases}-2 \space\space\space\space , \space\space\space\space x\leq 3\\ 2 \space\space\space\space\space , \space\space\space\space 3 <x\end{cases}\]

Determine the domain and range of ‘f’ and sketch its graph.

Solution:-

The domain of g is (-∞, +∞), following is the graph of the function;

Example#7

A piecewise function f is defined by;

\[f\left( x\right) =\begin{cases}1-x^{2} \space\space\space\space , \space\space\space\space x\angle 0\\ 3+x \space\space\space\space , \space\space\space\space 0\leq x\end{cases}\]

Determine the domain and range of ‘f’ and sketch its graph.

Solution:-

The domain of g is (-∞, +∞), following is the graph of the function;

This is a continuous graph having a range (-∞, +∞).

Example#8

A piecewise function f is defined by;

\[f\left( x\right) =\begin{cases}6x+7 \space\space\space\space , \space\space\space\space x\leq -2\\ 4-x \space\space\space\space , \space\space\space\space -2 <x\end{cases}\]

Determine the domain and range of ‘f’ and sketch its graph.

Solution:-

The domain of g is (-∞, +∞), following is the graph of the function;

The range is (-∞, 6).

Example#9

Sketch the graph of the signum function (or sign function), denoted by “sgn” and defined piecewise as below;

\[sgn\left( x\right) =\begin{cases}-1 \space\space\space\space , \space\space\space\space x <0\\ 0 \space\space\space\space , \space\space\space\space x=0\\ 1 \space\space\space\space , \space\space\space\space 0 <x\end{cases}\]

sgn x is read “signum of ‘x'”.

Solution:-

The domain of sgn x is (-∞, +∞). Following is the graph of sign (signum) function;

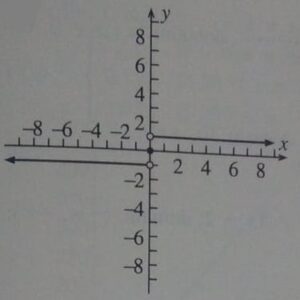
The range comprises mere three integers as mentioned in the question i.e. {-1, 0, 1}.

Example#10

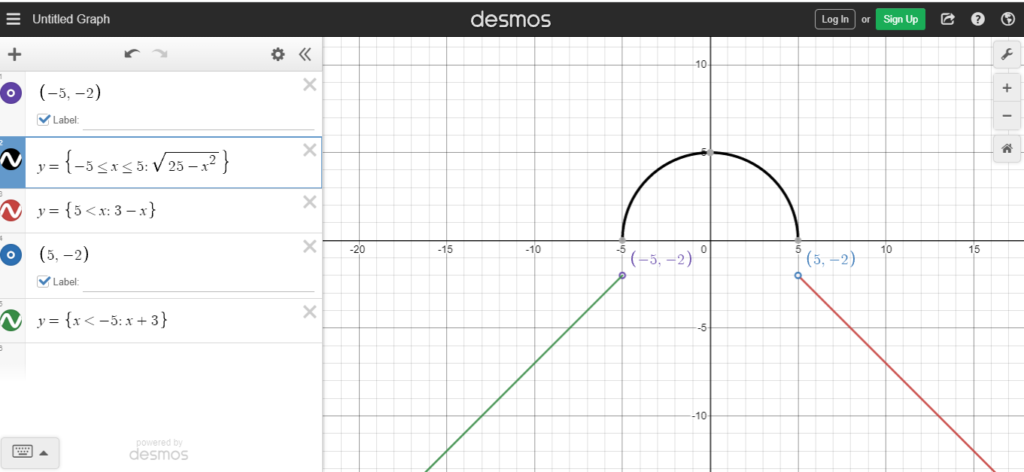
Sketch the graph and determine the domain and range of the following piecewise function h(x):

\[h\left( x\right) =\begin{cases}x+3 \space\space\space\space , \space\space\space\space x <-5\\ \sqrt{25-x^{2}} \space\space\space\space , \space\space\space\space -5\leq x\leq 5\\ 3-x \space\space\space\space , \space\space\space\space 5 <x\end{cases}\]

Solution:-

The domain is (-∞, +∞), following is how we have sketched the graph;

And the range is (-∞, -2) ∪ [0, 5].

How to use a piecewise function calculator to sketch its graph?

There are various online and downloadable graphing calculators available that facilitate users to sketch piecewise functions, few are as follows:

Desmos Graphing Calculator
Symbolab
TI-8 4
Mathlab (Get it on google play)

Learn how to use Desmos Graphing Calculator to sketch a piecewise function

Here I am going to elaborate on how to sketch piecewise function graphs using a Desmos graphing calculator?

In the above video, I have selected a few of the examples that were solved and sketched manually in this article, and input their piecewise definitions with corresponding domains in order to obtain their graph, I have picked Example#1 here and tried to substitute commands on Desmos interface, let’s try to understand step by step.

STEP#1

Open Desmos graphing calculator
Type first piecewise domain and then the particular function separated by “:”
Enclose this command in { } brackets.

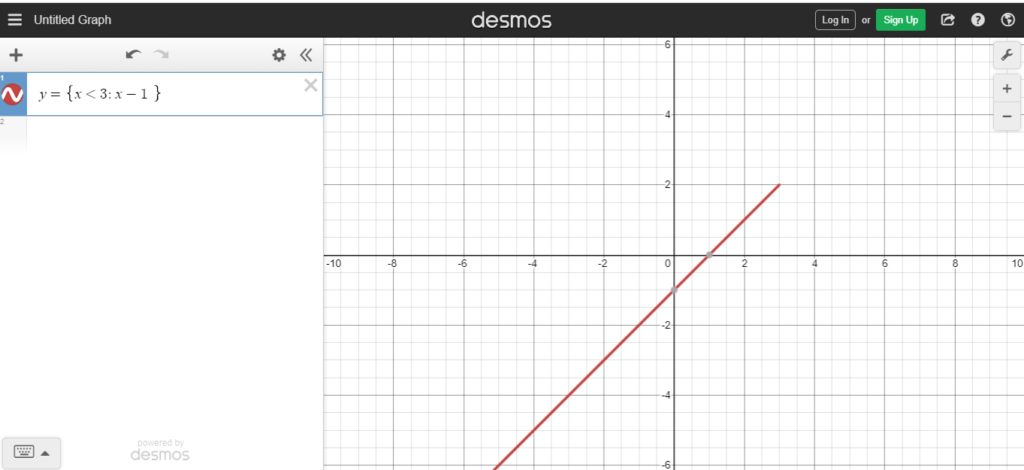
STEP#2

As ‘3’ is not included in the first piecewise domain “x<3” this means that the subjective graph does not contain (3, 2), so we have to develop a “hole” there, for this purpose;

Click on the “+” icon at the top right, this will open the next expression tab.
Type (3, 2)

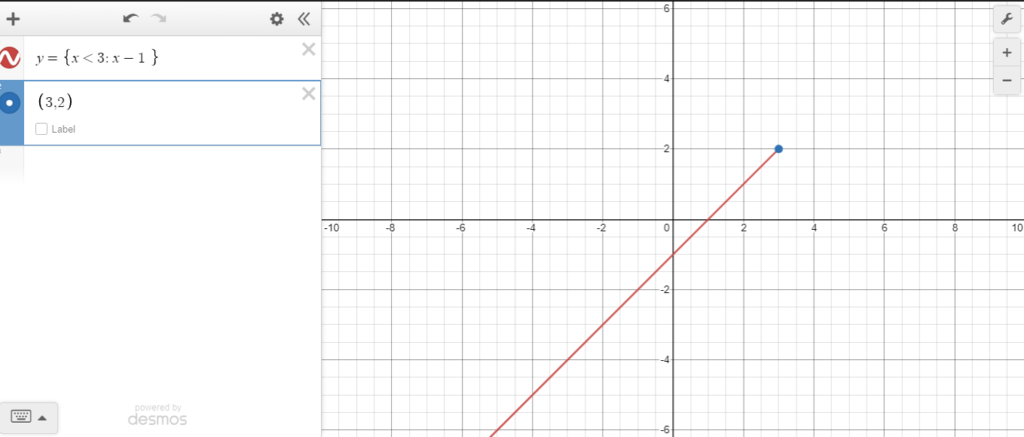
Press on the colorful circle next to (3,2), and you’ll get a panel from where you can select the hollow circle option.
Click on the hollow-point icon.

First piecewise is now accomplished.

STEP#3

Plot the point (3, 5), which was the second definition of the given piecewise function.
Keep it a solid point.

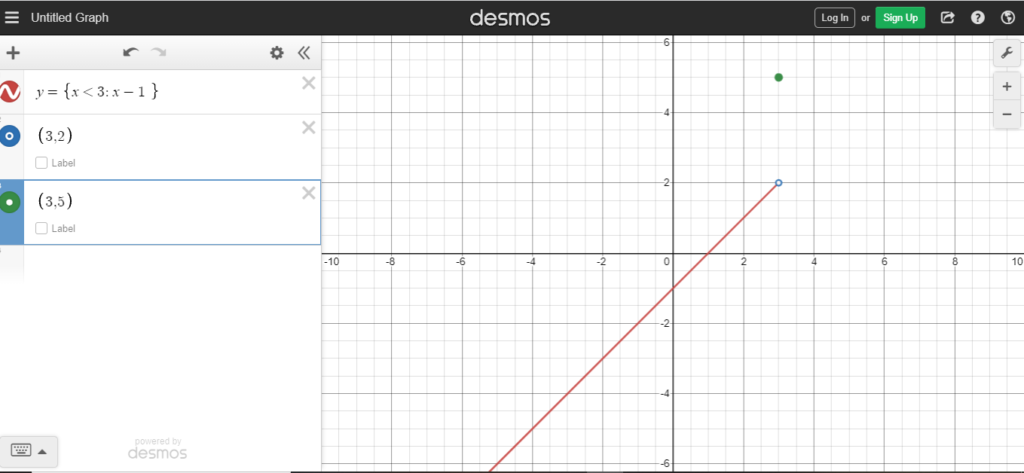
STEP#4

Finally type y= {3<x : 2x+1}
We will get another straight line representing the graph of f(x) = 2x+1 within the domain containing all values of x>3.

As “3” is not included in the domain of f(x)= 2x+1, so we are not going to include (3, 7).
Type (3,7) as another expression and make it a “hole”.

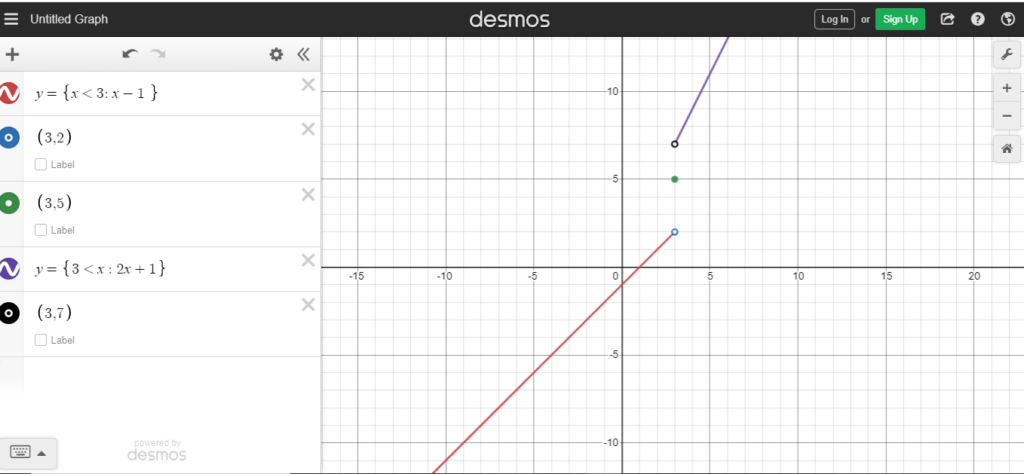
STEP#5

Let’s apply aforementioned strategies in Example#10

For more examples, you can watch my aforementioned video.

Uses and Applications of piecewise function

Piecewise functions in addition to Calculus magnanimously contribute to the mathematical modeling of various day-to-day real-life problems, which are later evaluated to get optimal and exact solutions. I have tried to compile some examples from the fields of accounting, Physics, Biology, etc, which would help you to get an idea about the applications and significance of piecewise functions.

In Denmark, income tax is assigned on the basis of income value, here f(x) is the function that represents the percentage of income that is deducted as tax, and ‘x’ defines the income value.

\[f\left( x\right) =\begin{cases}0 \space\space\space\space\space\space\space\space , \space\space\space\space x\angle \$ 10,000\\ 10\% \space\space\space\space , \space\space\space\space \$ 10,000\leq x\leq \$ 20,000\\ 15\% \space\space\space\space , \space\space\space\space \$ 20,000 >x\end{cases}\]

I am willing to order caps for “My Maths Club” students from “The Ware House”, Warehouse has charged me with respect to the following payment model which is expressed piecewise below;

\[C\left( x\right) =\begin{cases}7x \space\space\space\space , \space\space\space\space 0 <x <10\\ 5x \space\space\space\space ,\space\space\space\space 11\leq x\leq 50\\ 3x \space\space\space\space , \space\space\space\space x >50\end{cases}\]

Where C(x) is the total cost of caps, and ‘x’ is the number of caps so-ordered.

Most of the time, there is just one copy of each gene in the early stage of growth of a eukaryotic cell, which is represented as Ni-1. whereas in bacteria, there are multiple DNA plasmids in each cell (more than 100). Now for the sake of simplicity, it is assumed that before cell division, genes or DNAs including plasmid DNA are duplicated. Here we have symbolized the cycle period of cell division as “?”, thus, the following piecewise function can be used to explain cell volume factor v(t).

\[v\left( t\right) =\begin{cases}e^{\left( \dfrac{t}{T-k}\right) \ln 2} \space\space\space\space\space , \space\space\space\space\space k\leq t <k+1\\ 1\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space , \space\space\space\space\space t=k+1\end{cases}\]

A heavy-duty vehicle is moving on the highway with a variable velocity defined piecewise below;

\[v\left( t\right) =\begin{cases}5t \space\space\space\space , \space\space\space\space 0\leq t <15\\ 70 \space\space\space\space , \space\space\space\space 15\leq t <50\\ 250-3t \space\space\space\space , \space\space\space\space t\geq 50\end{cases}\]

Conclusion

Piecewise function is indeed a hallmark in the field of Calculus and is deeply involved in the concepts of limits, continuity, differential, and integral calculus. Beyond doubt, piecewise functions have simplified many complex targets of

Virtual strain fields
Artificial intelligence
Random field modeling
Optical Science
Pharmaceutical sciences (Pharmacokinetics)
Laser scanning for environmental sciences
Scientific Computation in Electrical Engineering
Sorting out issues in Geology and Mineralogy
Business, social, and life sciences

Everything, that we study in mathematics has its profound significance and substantial contribution in multifarious fields of real life, piecewise function is a clear example of this.

Q1) What is a piecewise function?

A piecewise function is a function that is defined by multiple pieces, each of which is defined over a different interval. The pieces of a piecewise function are typically joined together at points called breakpoints.

Q2) What are the properties of piecewise functions?

Piecewise functions have the following properties:

They are defined over a finite number of intervals.
The pieces of a piecewise function are joined together at points called breakpoints.
The value of a piecewise function is continuous at all breakpoints except for the last one.
The domain of a piecewise function is the union of the domains of the individual pieces.
The range of a piecewise function is the union of the ranges of the individual pieces.

Q3) What are some examples of piecewise functions?

Some examples of piecewise functions include:

The absolute value function
The greatest integer function
The step function
The triangle function
The sawtooth function

Q4) What are the applications of piecewise functions?

Piecewise functions are used in a variety of applications, including:

Computer graphics
Economics
Engineering
Physics
Biology
Medicine

Q5) Can piecewise functions be discontinuous?

A piecewise function can be discontinuous at any point where the two pieces of the function have different values. The discontinuity can be either removable or essential, depending on whether the function can be redefined at the breakpoint to remove the discontinuity.

Q6) How do I deal with discontinuities in a piecewise function?

There are two ways to deal with discontinuities in a piecewise function:

You can ignore the discontinuities and simply connect the points as smoothly as possible.
You can draw a gap at each discontinuity to indicate that the function is not defined at that point.

The best way to deal with discontinuities depends on the specific function and the application. If the function is only used for graphical purposes, then it may be acceptable to ignore the discontinuities. However, if the function is used for mathematical calculations, then it is important to draw a gap at each discontinuity.

Q7) How do I graph a piecewise function on a graphing calculator?

To graph a piecewise function on a graphing calculator, you need to first enter the definition of the function into the calculator. Then, you need to select the appropriate mode for graphing piecewise functions.

The specific steps for graphing a piecewise function on a graphing calculator vary depending on the calculator model. However, the general steps are as follows: